cpu逼近硬件浮点性能峰值

发表于 更新于 分类于 阅读次数： 本文字数： 6k 阅读时长 ≈ 5 分钟

SIMD

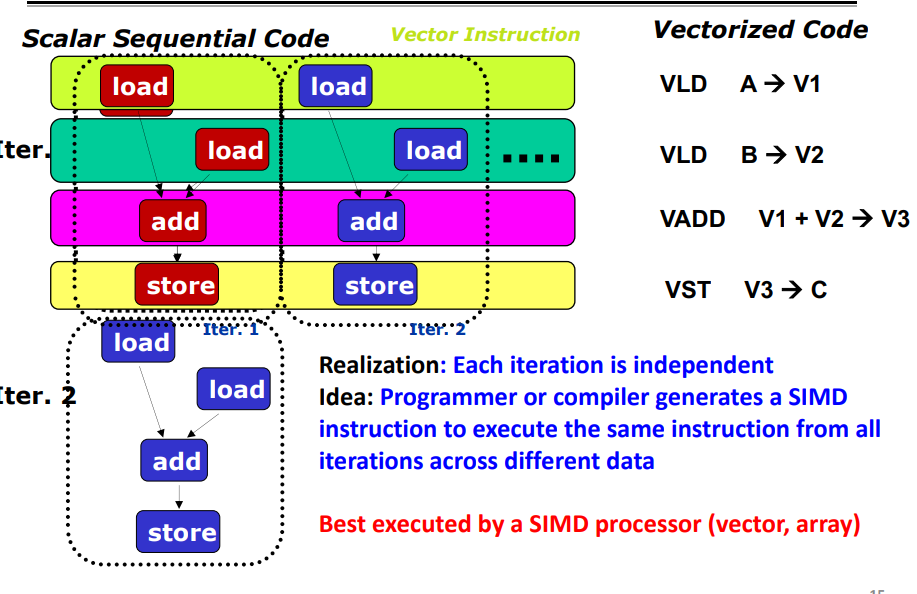
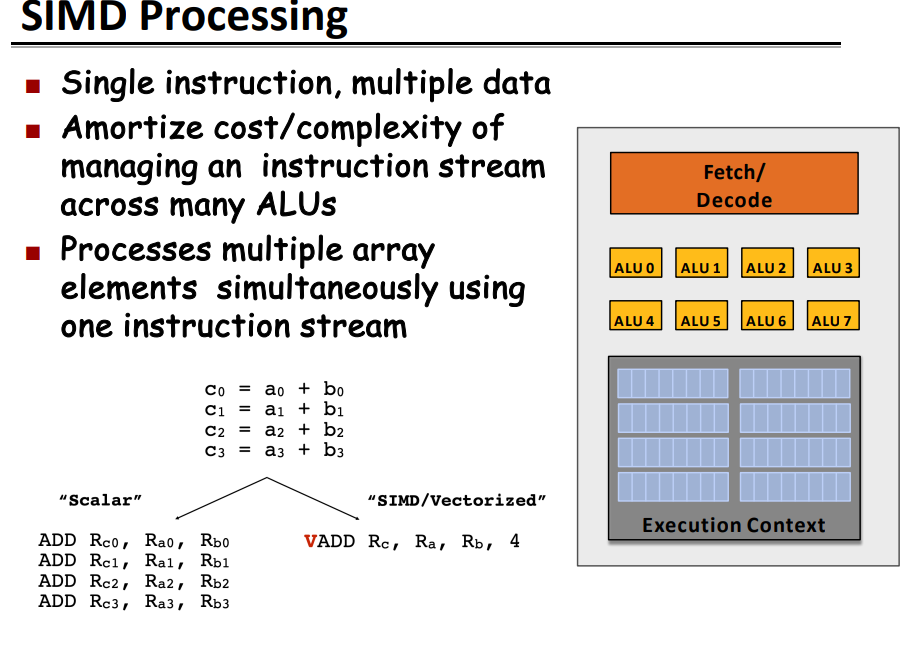
SIMD Processing (Single instruction, multiple data (SIMD))

它描述了具有多个处理元素(multiple processing elements)的计算机，可以在多个数据点(data points)上同时(simultaneously)完成相同的操作。

不是所有的算法都可以容易地被向量化.

硬件架构

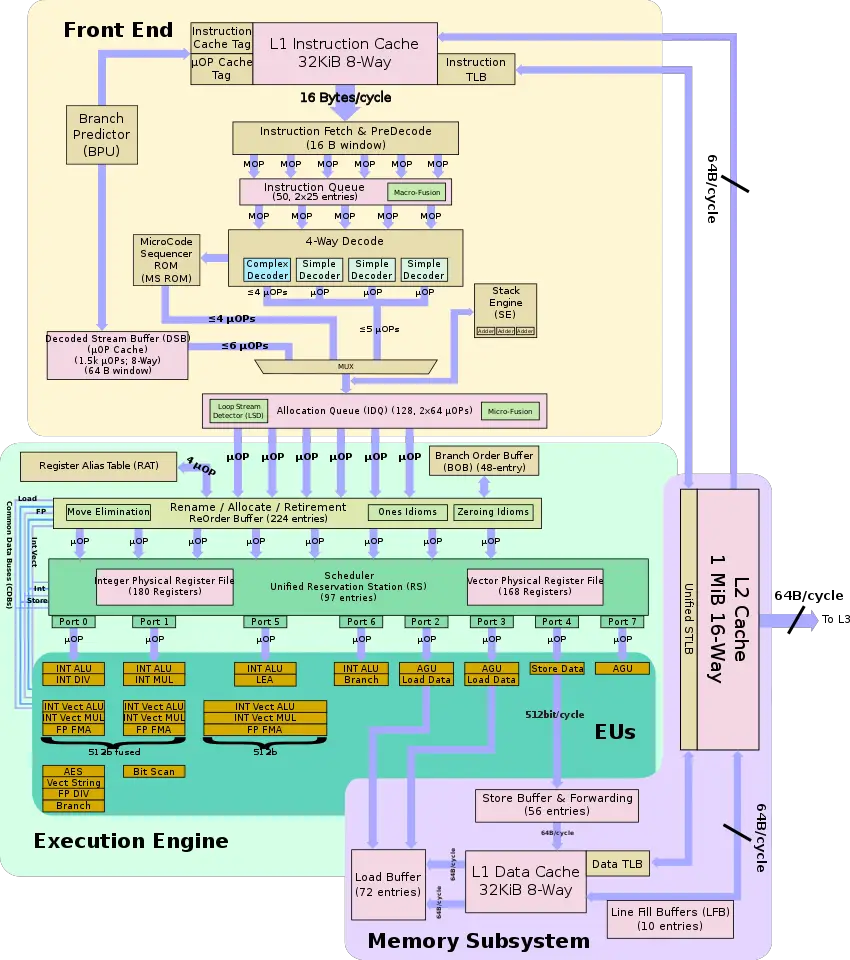
一个cycle有两个FMA单元，一个store单元

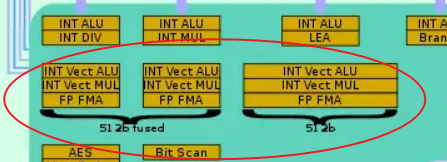
努力使FLOPS接近峰值

峰值计算公式：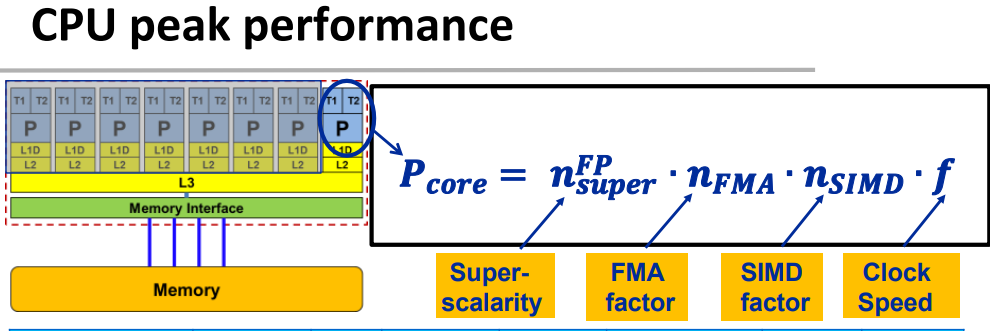

实验1：

计算很简单，但测量时间的部分很重要是linux特有的

**__rdtsc()**：

  • __rdtsc() 是一个内联汇编函数，用于获取当前处理器的时间戳计数（RDTSC）的值。
  • RDTSC 是一条 x86 指令，用于读取 CPU 时钟计数器的当前值，它是一个 64 位的计数器，记录了从 CPU 启动开始到现在的 CPU 时钟周期数。
1
2
3
uint64_t rdtsc(){
    return __rdtsc();
}

perf_event_open to get CPU clocks

perf_event_open(2) - Linux manual page (man7.org)

1
2
3
4
5
6
7
static long perf_event_open(struct perf_event_attr *hw_event, 
  pid_t pid, int cpu, int group_fd, unsigned long flags) {
  int ret;
  ret = syscall(SYS_perf_event_open, hw_event, pid, cpu,
                group_fd, flags);
  return ret;
}

该代码执行L*n个fma，几乎没有其他操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#if __AVX512F__
  const int vwidth = 64;
#elif __AVX__
  const int vwidth = 32;
#elif __SSE__ 
  const int vwidth = 16
#endif
  const int valign = sizeof(float);
  typedef float floatv __attribute__((vector_size(vwidth), aligned(valign)));
  const int L = sizeof(floatv) / sizeof(float);
...
      //time
  clock_gettime(CLOCK_MONOTONIC_RAW, &start);
  //cpu ref clocks
  start_cycle = rdtsc();
  //cpu core clocks
  ioctl(fd, PERF_EVENT_IOC_RESET, 0);
  ioctl(fd, PERF_EVENT_IOC_ENABLE, 0);
  asm volatile("#simd: ax+c loop begin");
  for (int i = 0; i < n; i++) {
    x = a * x + c;
  }
  asm volatile("#simd: ax+c loop end");
  ioctl(fd, PERF_EVENT_IOC_DISABLE, 0);
  end_cycle = rdtsc();
  clock_gettime(CLOCK_MONOTONIC_RAW, &end);
  double used_time = get_time(&start, &end);
  uint64_t used_cycles = end_cycle - start_cycle;
  double flops = 2.0 * L * n;
  if(read(fd, &cpu_clocks, sizeof(cpu_clocks)) == -1) {
    cout << "read cpu clocks error" << endl;
  }
...

  1. const int valign = sizeof(float);：

    • 这一行定义了一个常量 valign，其值等于 float 类型的大小。这个值通常用于向量类型的对齐，以确保向量在内存中按正确的边界对齐。

  2. typedef float floatv __attribute__((vector_size(vwidth), aligned(valign)));：

    • 这是一个 typedef 语句，用于定义一个名为 floatv 的新类型，它代表着一个向量类型。

    • float 表示向量中的元素类型。

    • ``` attribute((vector_size(vwidth), aligned(valign))) 

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      28
      29
      30
      31
      32
      33
      34
      35
      36
      37

            是 GNU C 扩展语法，用于指定向量的大小和对齐方式。

           - `vector_size(vwidth)` 表示向量的大小为 `vwidth`，即指定了向量的宽度。
           - `aligned(valign)` 表示向量的对齐方式为 `valign`，即指定了向量在内存中的对齐方式

      理论上，Cascade Lake支持AVx-512，一个cycle有两个FMA部件，理论峰值性能为：

      ![](./并行处理笔记lec2/image-20240318132045266.png)

      这里的频率使用的是cycle为单位，而不是秒为单位，因为一般电脑的负载在变换，每个cycle的时间是变化的

      所以这里采用的是reference clocks：

      ![](./并行处理笔记lec2/image-20240318134759456.png)

      编译：

      `g++ -D __AVX512F__ -march=native -O3 example1.cpp`

      运行：
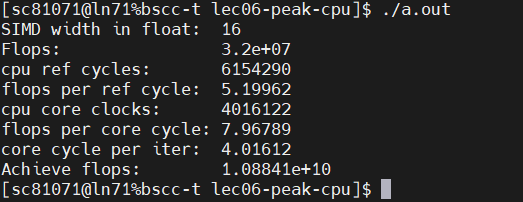
      ![](./并行处理笔记lec2/image-20240318134549327.png)

      性能达到了大概8 flops/core cycle，1/8 of the single core peak 64 flops/cycle

      ## 探究为什么没有到达峰值性能

      **首先在程序中放入汇编指令方便定位到循环的位置**

      ```cpp
      asm volatile ("#simd: ax+c loop begin");
      floatv a, x, c;
      for (int i = 0; i < n; i++) {
      x = a * x + c;
      }
      asm volatile ("#simd: ax+c loop end");

将其编译成汇编语言

g++ -D __AVX512F__ -march=native -O3 -S example1.cpp

See example1.s in your editor:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 90 "example1.cpp" 1
	#simd: ax+c loop begin
# 0 "" 2
#NO_APP
	vmovaps	-432(%rbp), %zmm1
	movl	$1000000, %eax
	.p2align 4,,10
	.p2align 3
.L13:
	vmovaps	-304(%rbp), %zmm4
	vfmadd132ps	-368(%rbp), %zmm4, %zmm1
	decl	%eax
	jne	.L13
	vmovaps	%zmm1, -304(%rbp)
#APP
# 94 "example1.cpp" 1
	#simd: ax+c loop end
# 0 "" 2

分析是否是循环造成的开销

进行8次循环展开：

外部循环，用于控制 SIMD 计算的次数。每次循环处理 8 个元素（因为 n / 8）。

#pragma GCC unroll 8

1
2
3
4
5
6
7
8
asm volatile ("# axpy simd begin");
  for (int i = 0; i < n / 8; i++) {
    #pragma unroll 8
    for(int j = 0; j < 8; j++) {
      x = a * x + c;
    }
  }
asm volatile ("# axpy simd end");

汇编：

1
2
3
4
5
6
7
8
9
10
11
12
13
.L13:
	vmovaps	-304(%rbp), %zmm4
	vfmadd132ps	-368(%rbp), %zmm4, %zmm1
	vfmadd132ps	-368(%rbp), %zmm4, %zmm1
	vfmadd132ps	-368(%rbp), %zmm4, %zmm1
	vfmadd132ps	-368(%rbp), %zmm4, %zmm1
	vfmadd132ps	-368(%rbp), %zmm4, %zmm1
	vfmadd132ps	-368(%rbp), %zmm4, %zmm1
	vfmadd132ps	-368(%rbp), %zmm4, %zmm1
	vfmadd132ps	-368(%rbp), %zmm4, %zmm1
	decl	%eax
	jne	.L13
	vmovaps	%zmm1, -304(%rbp)

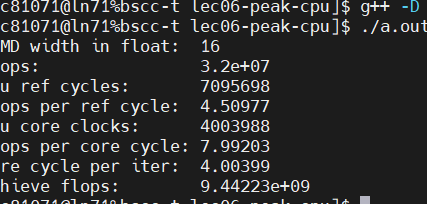
可以看出flops per cycle没有增加，说明不是循环的开销造成的

Cascade Lake内核每个周期可以执行两条vfmadd132ps指令

但是这并不意味着当前行vfmadd132ps的结果在下一个周期中可用于下一行的vfmadd132ps

每个周期两个vfmadd132ps表示吞吐量。每个指令有一个特定的延迟(>1个周期)

上面的指令之间存在相关性会造成阻塞。在我们的代码中，vfmadd使用前面的vfmadd的结果

软件优化策略： http://www.agner.org/optimize/

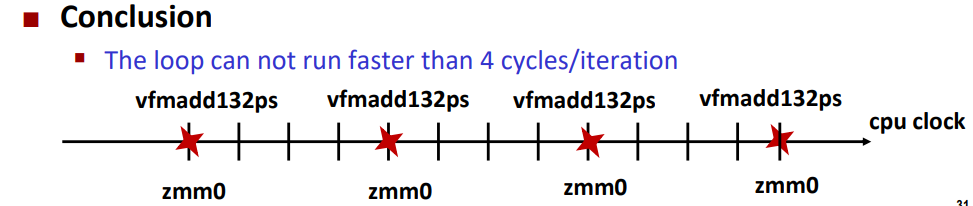
如何克服延迟

  • 增加并行性(没有其他方法)

  • 你不能让串行计算链运行得更快(如果你想改变算法)，您只能通过运行多个独立链来提高吞吐量

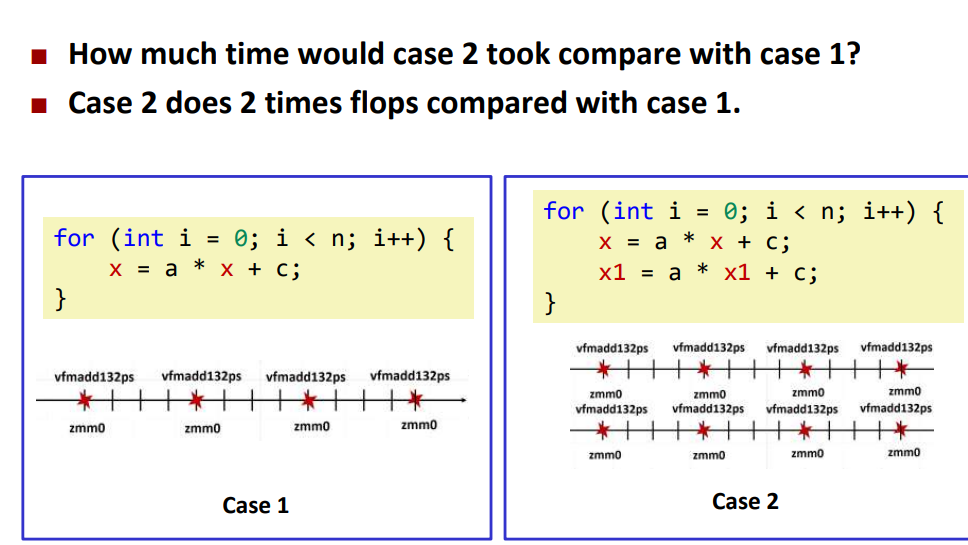
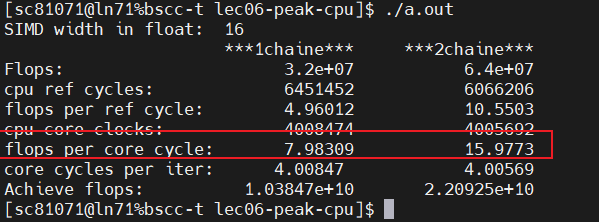
可以看出case2比case1快了一倍

之前我们分析过性能是理想性能的1/8所以，这里使用8个独立链条就能逼近峰值浮点性能

1
2
3
4
5
6
7
8
9
template<uint32_t nv> 
void axpy_simd(floatv *X, floatv a, floatv c){
  for(uint64_t i = 0; i < n; i++) {
#pragma unroll nv
    for(uint32_t j = 0; j < nv; j++) {
      X[j] = a * X[j] + c;
    }
  }
}

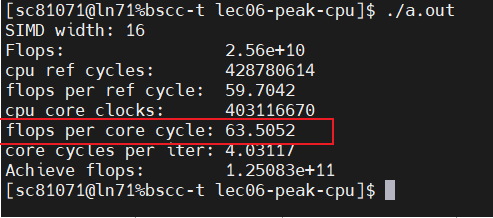
可以看出逼近了理想的峰值性能

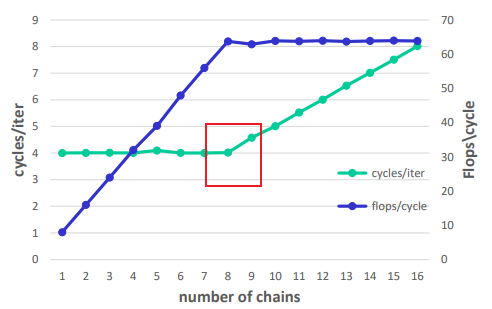
链条数对flops/cycle的影响：

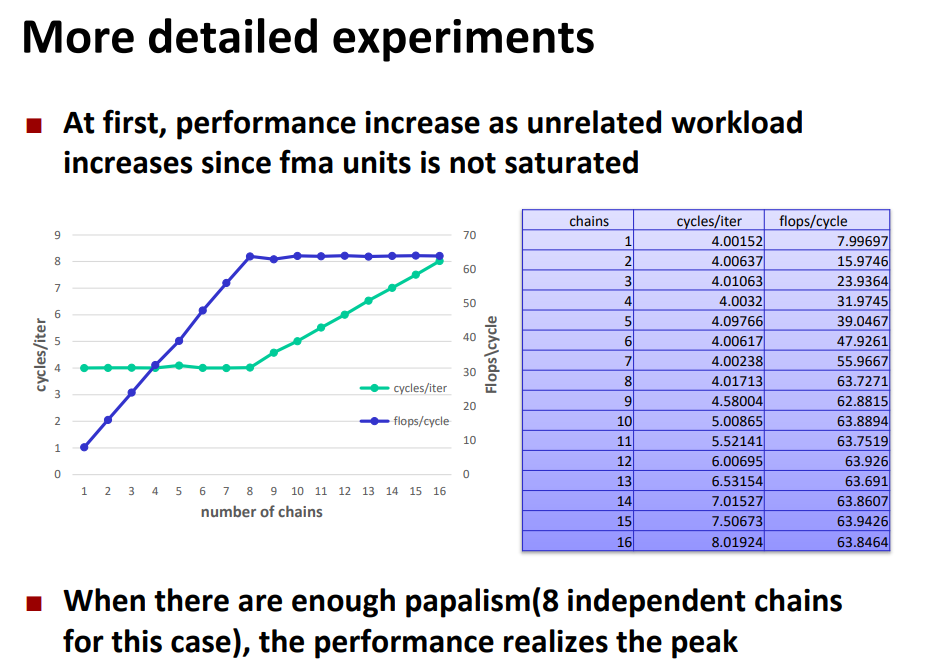
超标量处理器上的性能

依赖关系（ dependency)

依赖关系限制了计算进行的速度，即使存在无限数量的执行资源.

增加独立计算的数量会增加吞吐量，直到达到执行资源的限制

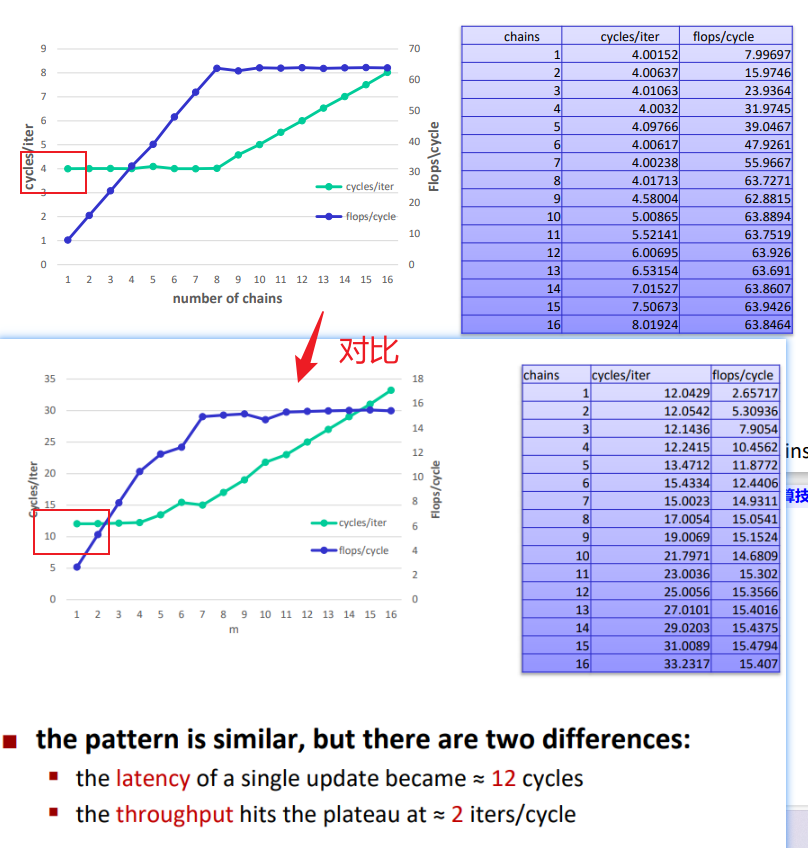
分析吞吐量

当独立的链条数值是一个变量会发生什么

对比两个程序的汇编代码：

多了 vmovaps操作，也就是说：代码现在涉及加载/存储的问题

由于执行资源的原因，所有指令都有自己的吞吐量限制(就像FMA一样)

吞吐量=可以按周期执行的指令的数量，“每个周期两个vfmadds”只是其中的一个例子

Dispatch ports

each instruction(u-op)通过分派端口分派到特定的执行单元

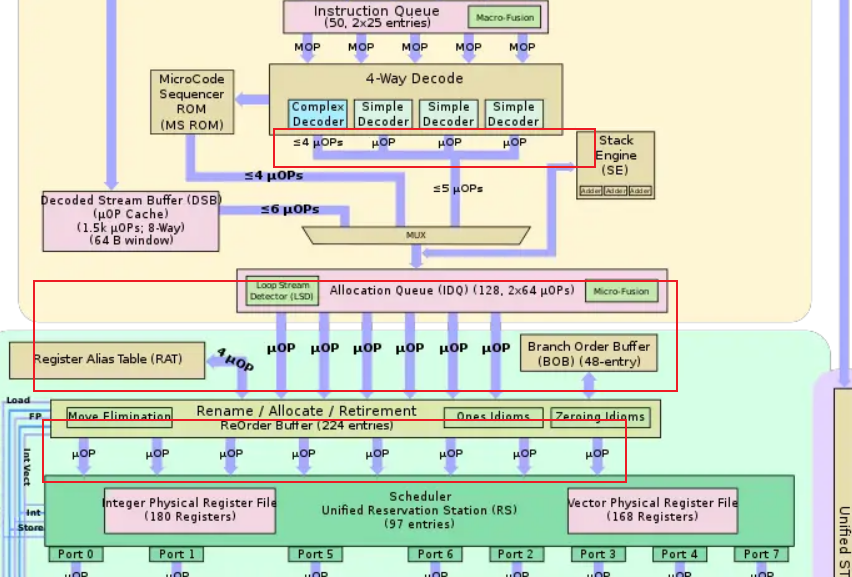
吞吐量的限制

2个fma /cycle意味着有2个端口可以处理fused fma,一条指令的吞吐量受能处理它的端口数量的限制

Buckets effect

吞吐量 may be bounded by one type instruction:例如

▪ Bounded by FMA, good, peak performance

▪ Bounded by others, e.g., store, may limit the performance

一个好用的分析throughput的工具：Intel® Architecture Code Analyzer

How to overcome the throughput limit

我们的目标是实现 two iterations/cycle (throughput limit of FMA)（达到FMA的throughput）

当前的瓶颈是：the bottleneck is a store instruction (1/cycle)

首先要避免在每一个单独的fmadd操作时进行loading/storing data的工作

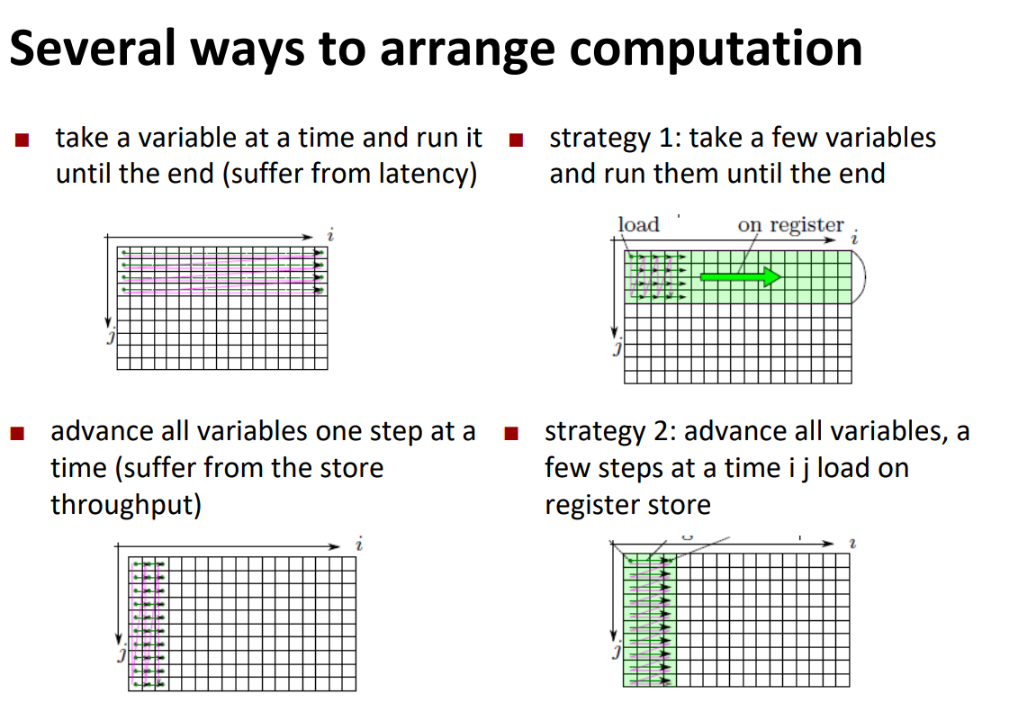
第一种方案是加载一个内层变量然后执行外层循环，执行完一遍再加载下一个内层变量，这样的问题是没有充分利用独立链条，程序收到latency的限制，解决方案是strategy1 ，一次多加载几个内层变量。

第二种解决方案是一次加载全部的内层变量然后再执行外层循环。这样的限制是访存端的throughoutput

解决方案是strategy2

实现strategy1

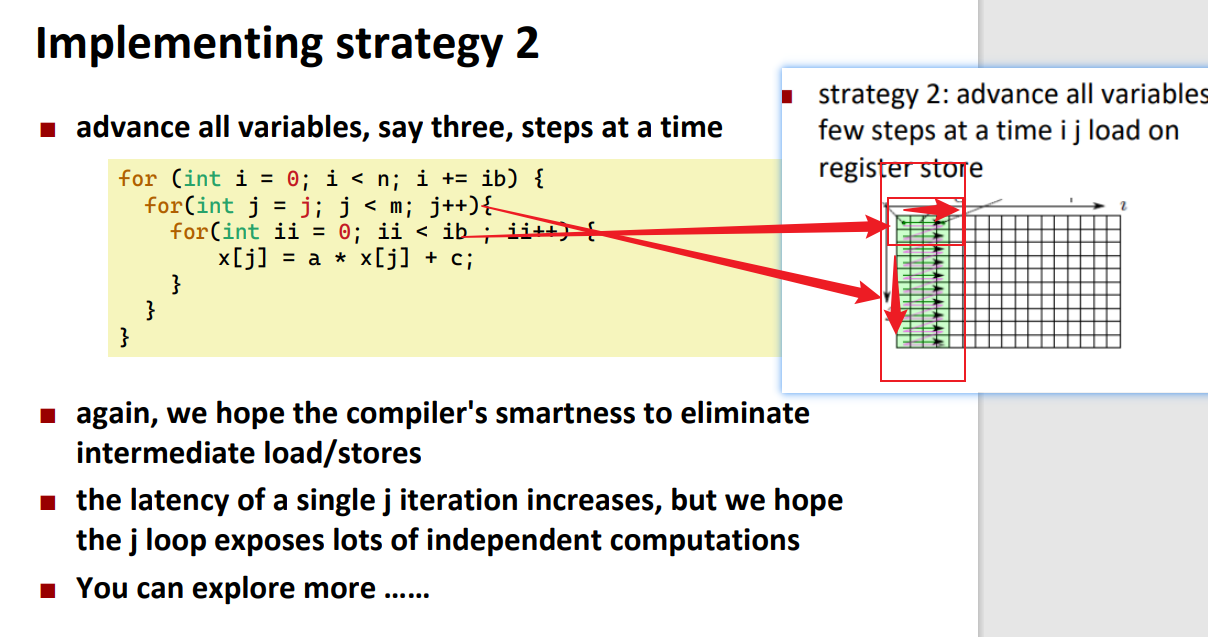
我们希望它通过第i循环(第2行)只加载/存储每个变量一次!。这种编码依赖于编译器的聪明程度

1
2
3
4
5
6
7
8
9
10
11
12
const int n = 1000000;
template <unsigned int jb>
void axpy_simd(floatv *X, floatv a, floatv c, long 
m){
for(uint32_t j = 0; j < m; j += jb) {
for(uint64_t i = 0; i < n; i++) {
#pragma unroll jb
for(uint32_t jj = j; jj < j + jb; jj++) {
X[jj] = a * X[jj] + c;
}
}
}}

我们帮助编译器进行优化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
template <unsigned int jb>
void axpy_simd_register(floatv *X, floatv a, floatv c, long m){
__m512 tmp[jb];
for(uint32_t j = 0; j < m; j += jb) {
//load into register
#pragma unroll jb
for(uint32_t jj = 0; jj < jb; jj++) {
tmp[jj] = X[jj + j];
}
//compute
for(uint64_t i = 0; i < n; i++) {
#pragma unroll jb
for(uint32_t jj = 0; jj < jb; jj++) {
tmp[jj] = a * tmp[jj] + c;
}
}
//write back
for(uint32_t jj = 0; jj < jb; jj++) {
X[jj + j] = tmp[jj];
}
}
}

Implementing strategy 2