二叉搜索树
二叉搜索树的中序遍历是有序的。
中序遍历的利用
JZ36
二叉搜索树与双向链表
充分利用中序遍历的有序性构造有序的双向链表。
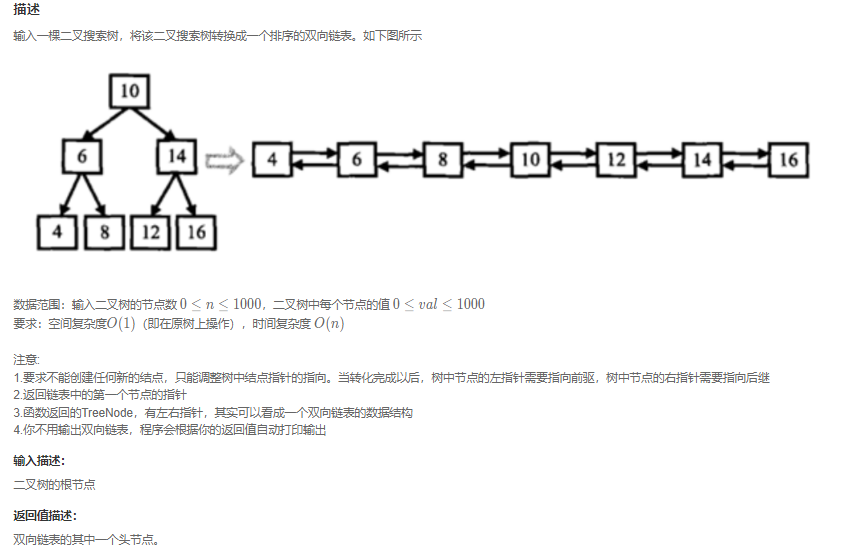
改造原始的中序遍历,避免构造额外的空间。核心的逻辑是:左中右中,中的前驱是左,后继是右子树。所以可以使用一共pre指针指向左节点,然后root的left指向pre,pre的right指向root。pre更新到root,pre设置为全局的变量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class Solution {
public:
TreeNode * pre;
TreeNode* Convert(TreeNode* pRootOfTree) {
if(pRootOfTree==nullptr){
return nullptr;
}
pre=nullptr;
TreeNode * ret;
ret=pRootOfTree;
while(ret->left!=nullptr){
ret=ret->left;
}
inorder(pRootOfTree);
return ret;
}
void inorder(TreeNode * root){
if(root->left!=nullptr){
inorder(root->left);
}
root->left=pre;
if(pre!=nullptr){
pre->right=root;
}
pre=root;
if(root->right!=nullptr){
inorder(root->right);
}
}
};
|
JZ8
二叉树的下一个结点
描述:
给定一个二叉树其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的next指针
要求:**空间复杂度 O*(1) **,时间复杂度 O(n)
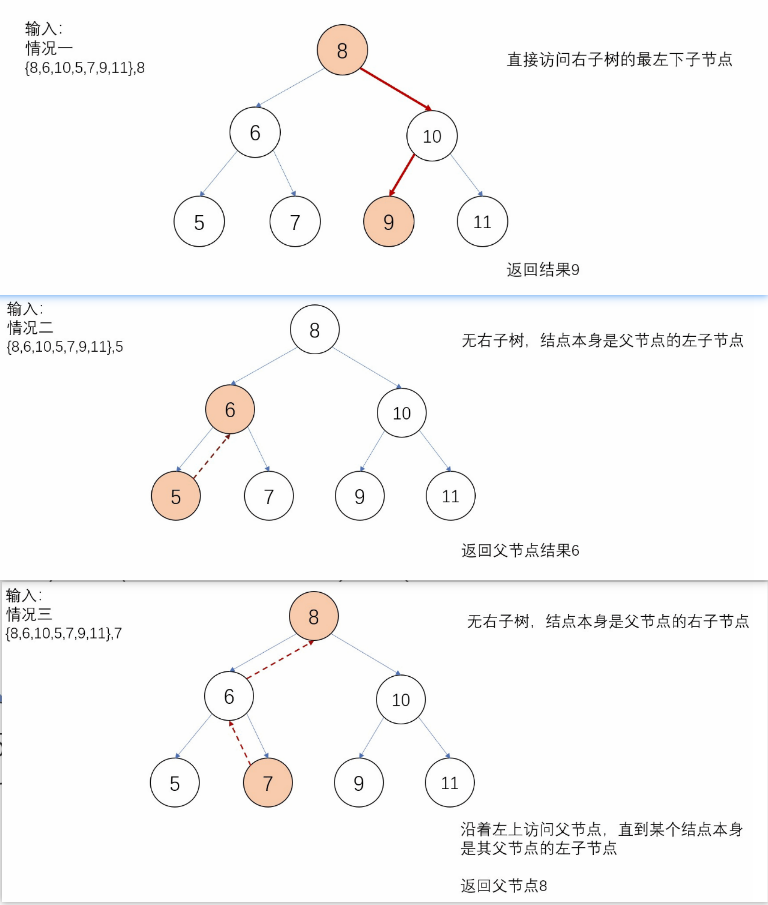
分析可能存在的三种情况:
- 如果给出的结点有右子节点,则最终要返回的下一个结点即右子树的最左下的结点
- 如果给出的结点无右子节点,且当前结点是其父节点的左子节点,则返回其父节点
- 如果给出的结点无右子节点,且当前结点是其父节点的右子节点,则先要沿着左上方父节点爬树,一直爬到当前结点是其父节点的左子节点为止,返回的就是这个父节点;或者没有满足上述情况的则返回为NULL
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
class Solution {
public:
TreeLinkNode* GetNext(TreeLinkNode* pNode) {
if(pNode==nullptr)
return nullptr;
if(pNode->right!=nullptr){
TreeLinkNode* cur=pNode->right;
TreeLinkNode* pre=cur;
while(cur!=nullptr){
pre=cur;
cur=cur->left;
}
return pre;
}
if(pNode->next==nullptr)
return nullptr;
if(pNode->next->left==pNode){
return pNode->next;
}
TreeLinkNode* cur=pNode;
while(cur->next!=nullptr&&(cur!=cur->next->left)){
cur=cur->next;
}
if(cur==cur->next->left)
return cur->next;
else
return nullptr;
}
};
|
利用搜索二叉树的有序性
JZ68
二叉搜索树的最近公共祖先

解答:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class Solution {
public:
int lowestCommonAncestor(TreeNode* root, int p, int q) {
queue<TreeNode *>myqueue;
myqueue.push(root);
int rettmp;
int minnum=min(p,q);
int maxnum=max(p,q);
TreeNode *cur=root;
while (cur!=nullptr) {
if(maxnum<cur->val)
cur=cur->left;
else if(minnum>cur->val)
cur=cur->right;
else if(cur->val>=minnum&&cur->val<=maxnum){
rettmp=cur->val;
break;
}
}
return rettmp;
}
};
|
JZ86
在二叉树中找到两个节点的最近公共祖先
递归思路:
分析遍历到任意的一个结点(之前没有找到过那两个结点),可能的情况分为四类:
- 该节点的左树上没找到目标节点---》说明结果在右子树上,继续遍历右子树
- 该节点的右树上没找到目标节点---》说明结果在左子树上,继续遍历左子树
- 该节点的左树上找到了目标节点,右边也找到了节点---》返回该节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public:
int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
TreeNode * ret=subtask(root,o1,o2);
return ret->val;
}
TreeNode * subtask(TreeNode* root, int o1, int o2){
if(root==nullptr||root->val==o1||root->val==o2){
return root;
}
TreeNode *left=subtask(root->left, o1, o2);
TreeNode * right=subtask(root->right,o1,o2);
if(left==nullptr){
return right;
}
if(right==nullptr){
return left;
}
return root;
}
};
|
本题还可以使用hashmap和hashset暴力求解(思路比较简单此处不做陈述)
这种用hashmap记录的一条可以反向回去的链条的方法也是比较经典值得思考的。
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include <unordered_map>
class Solution {
public:
int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
unordered_map<int,int> mymap;
mymap[root->val]=-1;
queue<TreeNode *>myqueue;
myqueue.push(root);
TreeNode * cur;
while(!myqueue.empty()&&(mymap.find(o1)==mymap.end()||mymap.find(o2)==mymap.end())){
cur=myqueue.front();
myqueue.pop();
if(cur->left!=nullptr){
mymap[cur->left->val]=cur->val;
myqueue.push(cur->left);
}
if(cur->right!=nullptr){
mymap[cur->right->val]=cur->val;
myqueue.push(cur->right);
}
}
unordered_set<int> ancestor;
int curnum=o1;
while(mymap.find(curnum)!=mymap.end()){
ancestor.insert(curnum);
curnum=mymap[curnum];
}
curnum=o2;
while(ancestor.find(curnum)==ancestor.end()){
curnum=mymap[curnum];
}
return curnum;
}
};
|
利用层次遍历
JZ28
对称的二叉树
给定一棵二叉树,判断其是否是自身的镜像(即:是否对称)
对称的二叉树每一层都是回文的情况。那我们从左往右遍历一层(包括空节点),和从右往左遍历一层(包括空节点),应该得到相同的结果。而且我们不需要两个层次遍历都完整地遍历二叉树,只需要一半就行了,从左往右遍历左子树,从右往左遍历右子树,各自遍历一半相互比对,因为遍历到另一半都已经检查过了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
|
class Solution {
public:
bool isSymmetrical(TreeNode* pRoot) {
queue<TreeNode*> myqueue1,myqueue2;
if(pRoot==nullptr)
return true;
myqueue1.push(pRoot->left);
myqueue2.push(pRoot->right);
int num=1;
int numnew=0;
while(!myqueue1.empty()){
if(myqueue2.empty()){
return false;
}
while(num!=0){
num--;
TreeNode * cur1=myqueue1.front();
TreeNode * cur2=myqueue2.front();
myqueue1.pop();
myqueue2.pop();
if(cur1==nullptr&&cur2==nullptr){
continue;
}
if((cur1==nullptr&&cur2!=nullptr)||(cur1!=nullptr&&cur2==nullptr))
return false;
if(cur1->val!=cur2->val)
return false;
if(cur1->left!=nullptr&&cur2->right!=nullptr){
myqueue1.push(cur1->left);
myqueue2.push(cur2->right);
numnew++;
}
if(cur2->left!=nullptr&&cur1->right!=nullptr){
myqueue2.push(cur2->left);
myqueue1.push(cur1->right);
numnew++;
}
if((cur2->left==nullptr&&cur1->right!=nullptr)||(cur2->left!=nullptr&&cur1->right==nullptr)||(cur1->left==nullptr&&cur2->right!=nullptr)||
( cur1->left!=nullptr&&cur2->right==nullptr))
return false;
}
num=numnew;
numnew=0;
}
return true;
}
};
|
路径和问题
JZ82
二叉树中和为某一值的路径(一)
只判断路径是否存在的:
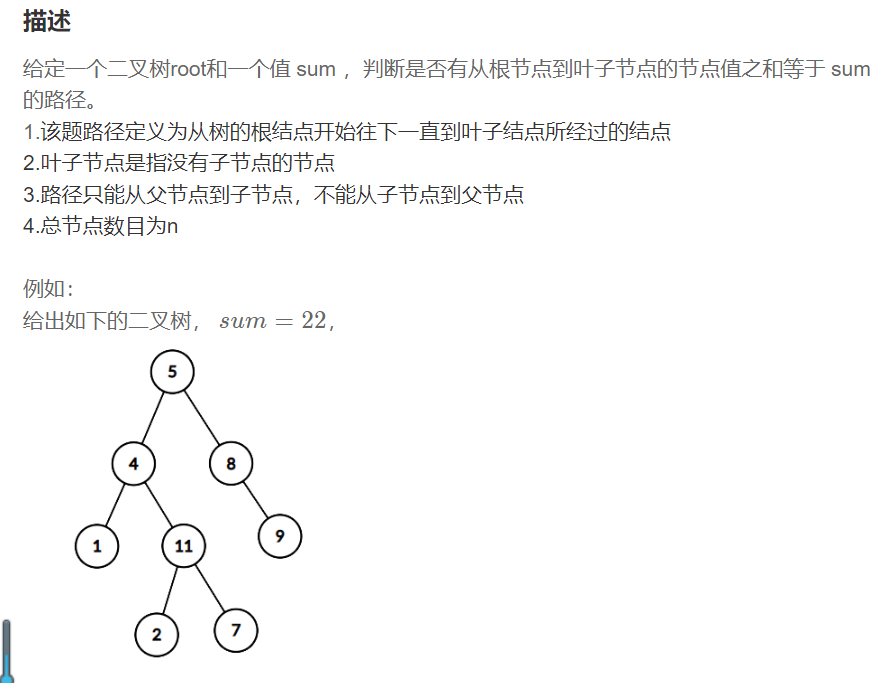
使用简单的递归就可以解决:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
if(root==nullptr){
return false;
}
return subtask(root,sum);
}
bool subtask(TreeNode* root, int sum) {
if(root->left==nullptr&&root->right==nullptr){
if(sum-root->val==0)
return true;
else
return false;
}
bool lefttry=false;
bool righttry=false;
if(root->left!=nullptr)
lefttry=subtask(root->left, sum-root->val);
if(root->right!=nullptr)
righttry=subtask(root->right, sum-root->val);
return lefttry||righttry;
}
};
|
JZ34
二叉树中和为某一值的路径(二)
进阶版本,需要给出所有的路径,需要用深度优先搜索有恢复现场的步骤
这个在DFS深度优先搜索博文中介绍过,如下链接:
解析博客
JZ84
二叉树中和为某一值的路径(三)
不再限制是不是从根节点到叶子节点的路径。要计算路径的数量
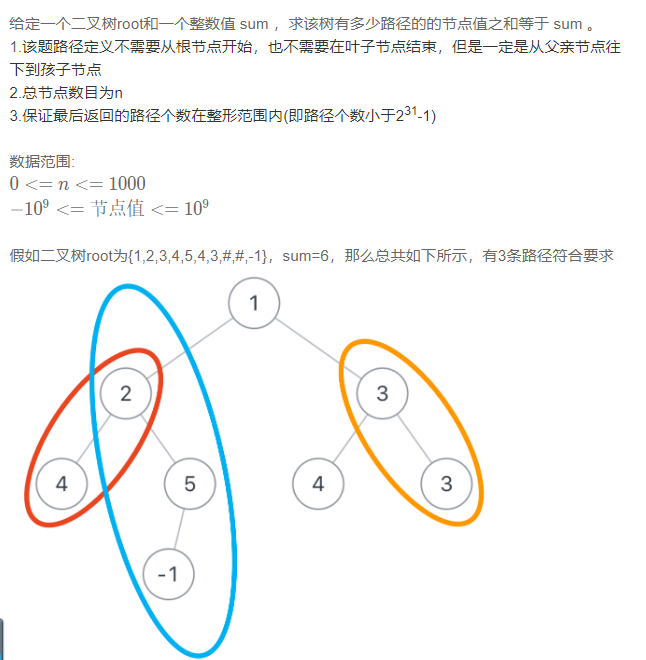
感觉有点动态规划的意思,不过这里不用改成动态规划,用递归解决即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
#include <cstdio>
class Solution {
public:
int FindPath(TreeNode* root, int sum) {
if(root==nullptr)
return 0;
int ret=0;
ret+=subtask(root, sum);
if(root->right!=nullptr)
ret+=FindPath(root->right,sum);
if(root->left!=nullptr)
ret+=FindPath(root->left,sum);
return ret;
}
int subtask(TreeNode * root ,int target){
int ret=0;
if(root==nullptr)
return 0;
target-=root->val;
if(target==0)
ret++;
ret+=subtask(root->right,target);
ret+=subtask(root->left,target);
return ret;
}
};
|





