运算部件
运算部件
定点补码加法器设计
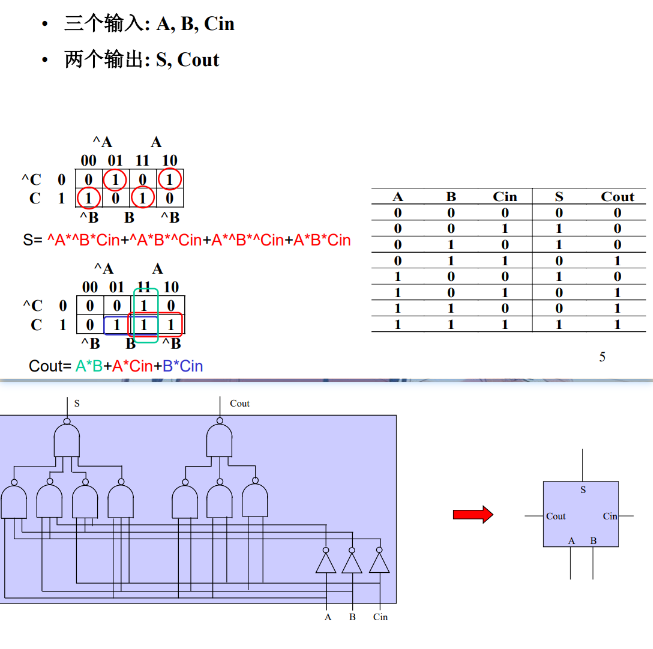
全加器
全加器的S有三级门延迟,cout端有两级门延迟。
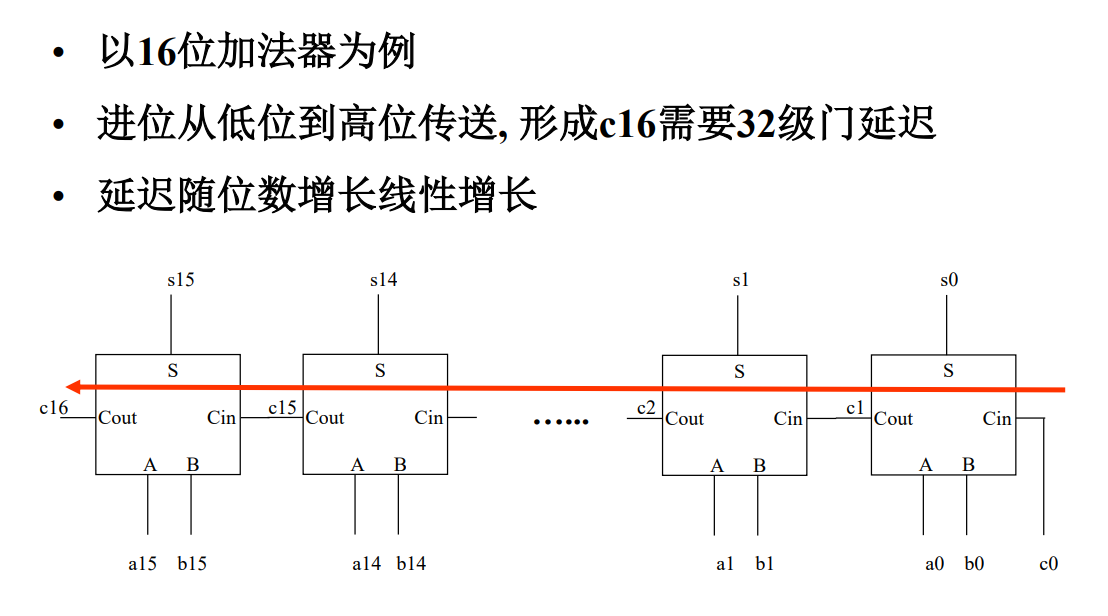
串行进位加法器
先行进位加法器
进位的传递
\(g_i\) 是进位生成因子。当相加的两位为1的时候才会产生进位因此:\(g_i=a_i*b_i\)
\(p_i\)是进位传递因子,当相加的两位有一个为1的时侯上一级的进位可以传递到下一级,因此\(p_t=a_i+b_i\)
此时有:\(c_{i+1}=pi+g_i*ci\)
4位并行进位逻辑

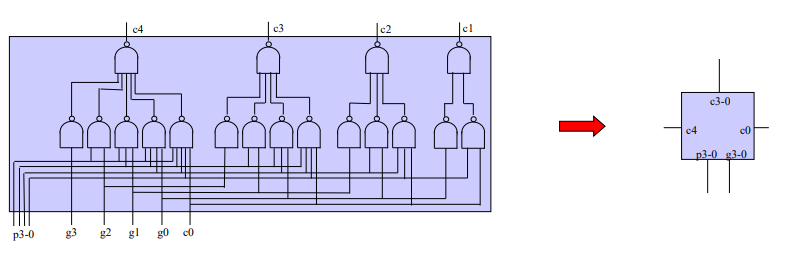
此时可以实现块内并行
块间并行
思路
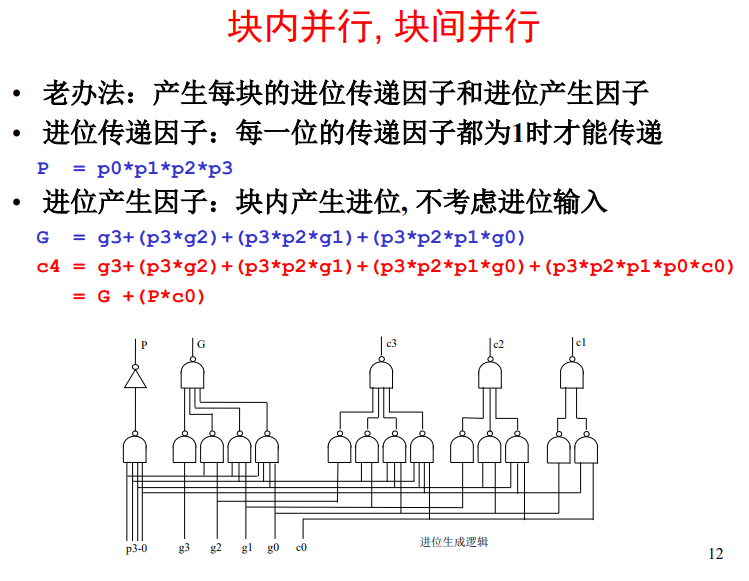
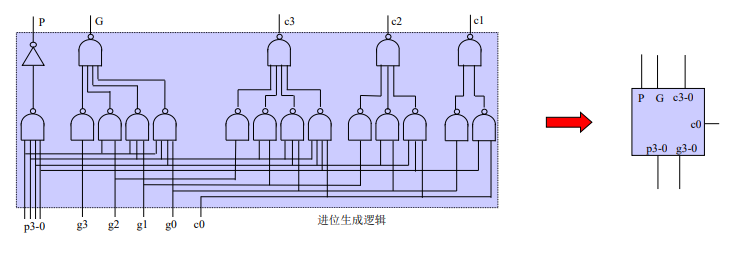
块间并行加法器
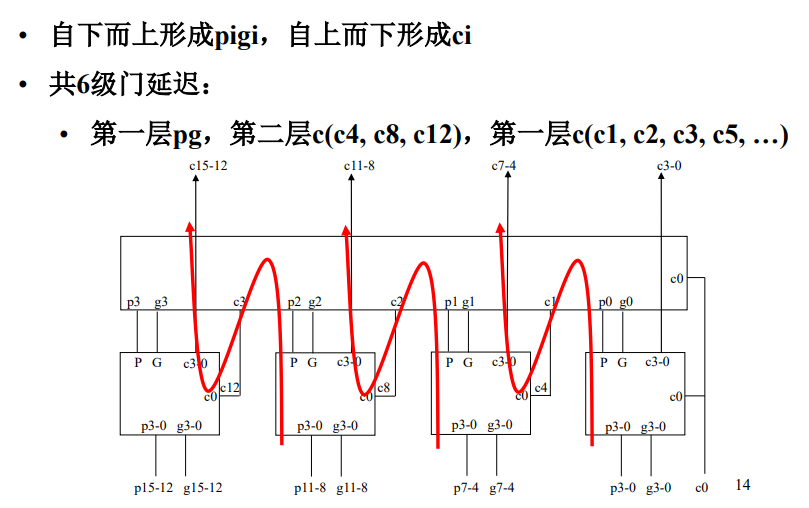
如上图所示,首先a和b生成p,g需要两级门延迟。第一层的p生成第二级的p0-p3,g0-g3输入需要两级门延迟,然后第二层级的p0-p3和C0生成c1-c3(也就是第一级的c4,c8,c12)需要两级门延迟。最后第一级根据c4,c8,c12,生成c4-c15.需要两级门延迟,一共是8级门延迟。如果是生成16位加法器的s15.需要c15与a15,b15经过全加器得到需要3级门延迟。一共是11级门延迟。
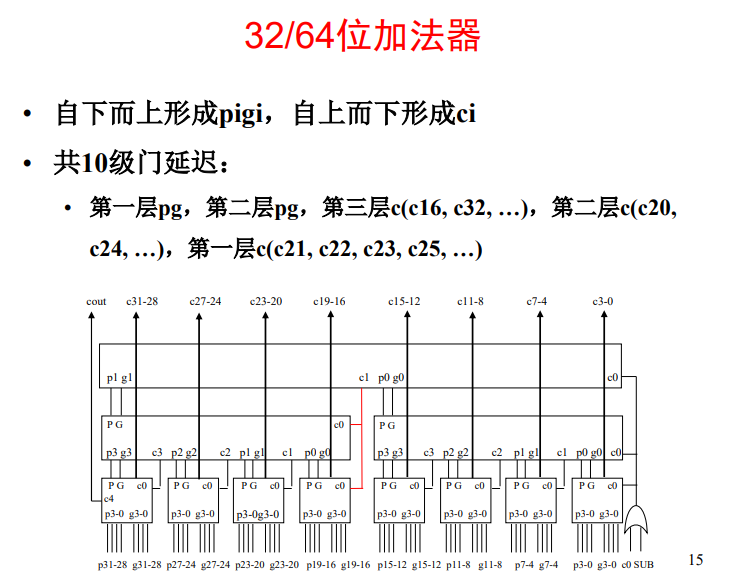
同理如果是得到s31需要10+2+3=15级门延迟
加法器的verilog实现
1 | module add16(a, b, cin, out, cout); |
1 | module C4(p,g,cin,P,G,cout) |
BOOTH乘法器
补码乘法原理

Booth算法

Booth二位一乘算法
对于16位乘法一位Booth算法还是需要计算32个数的加法,使用二位一乘后加法只需要进行16个数的相加。
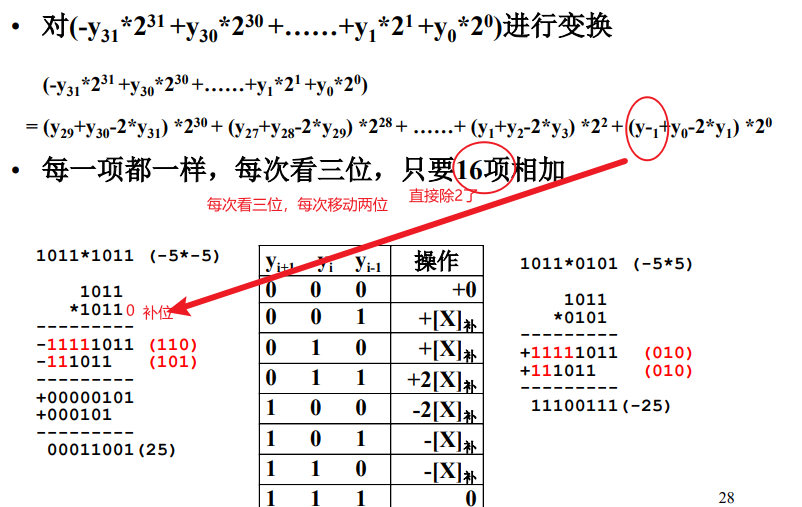
Booth两位乘电路
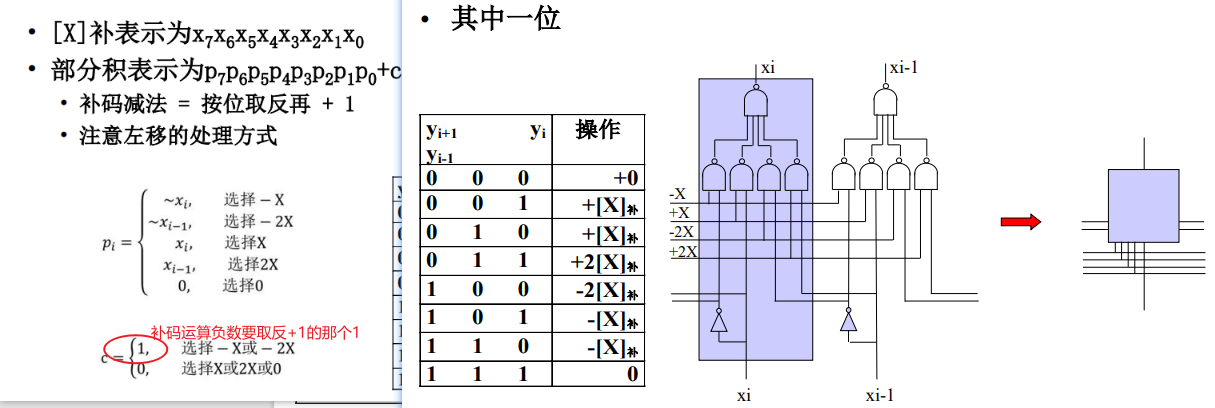
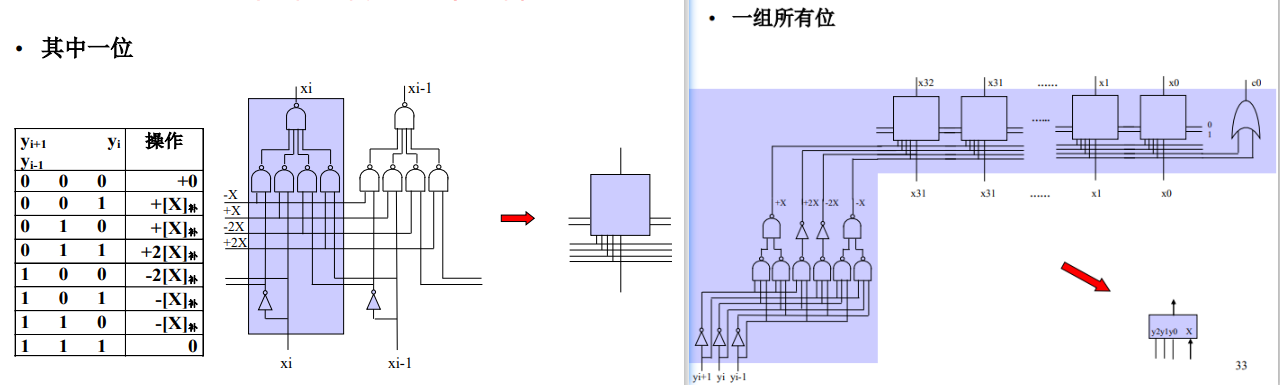
华莱士树
利用全加器减小加法数量,全加器把三个加数变成两个加数
基本思想

结构
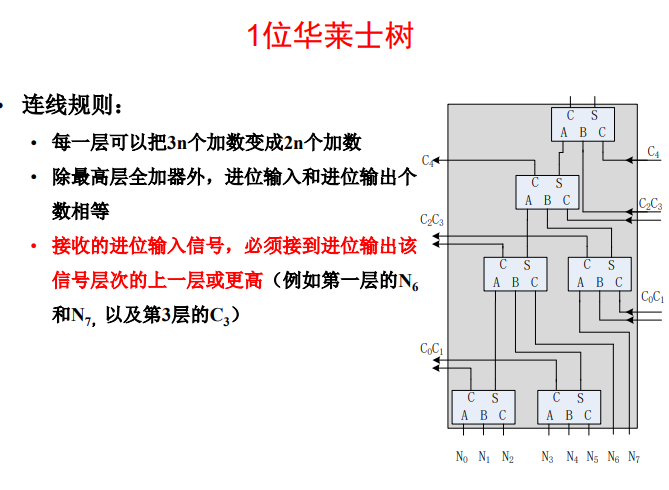
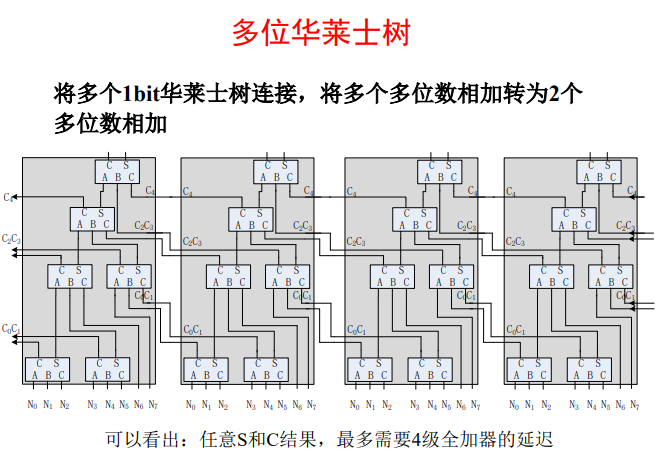
华莱士树进位连接要求 :进位输入信号必须接到进位输出该信号层次的上一层或更高
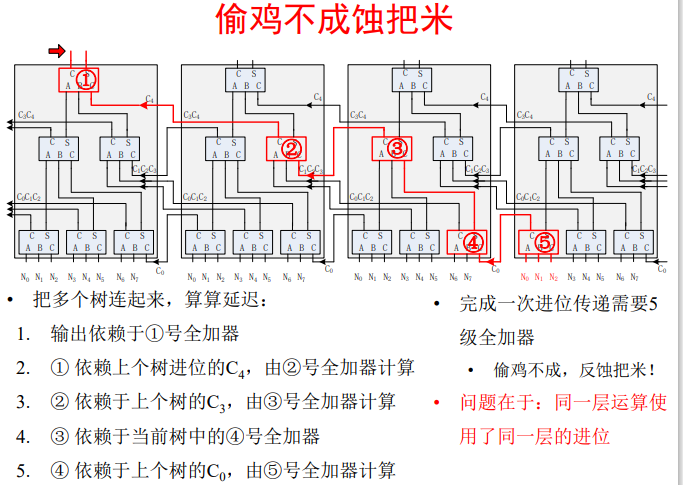
不这样连接的后果:
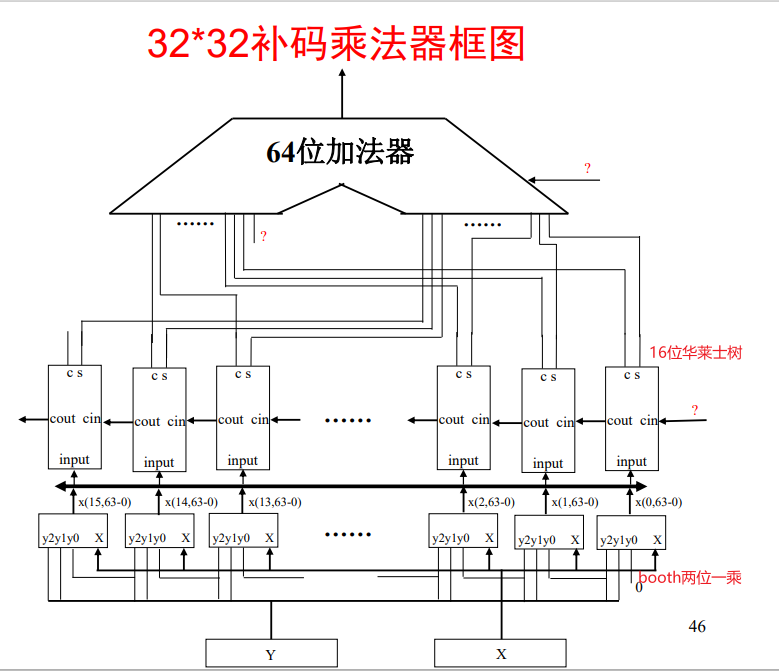
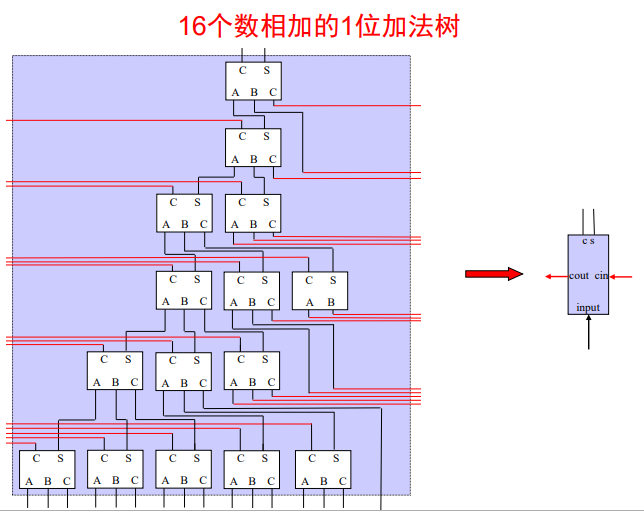
16位华莱士树
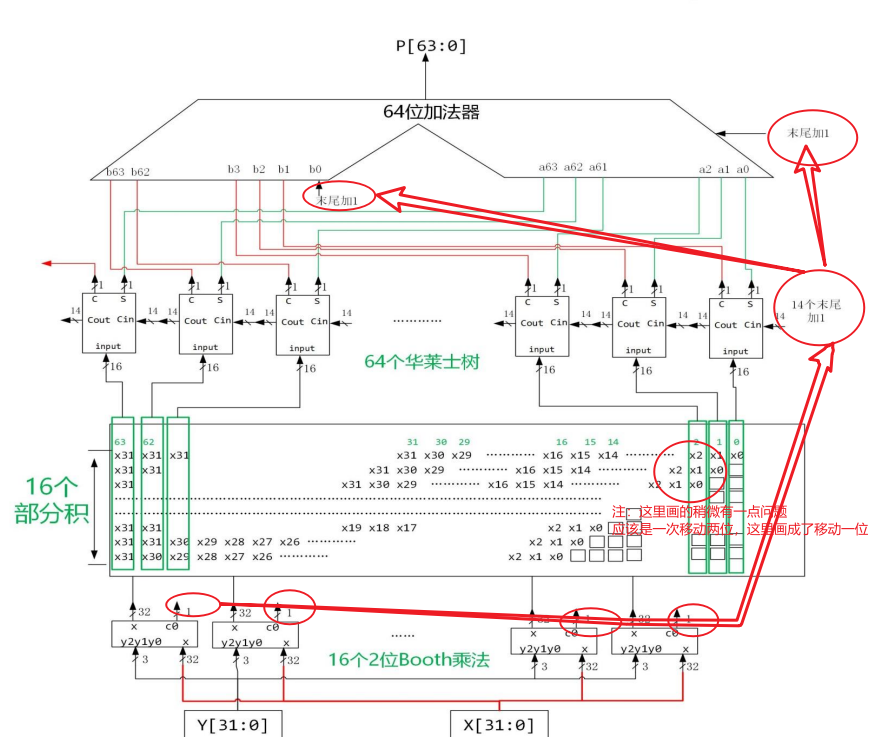
32位定点补码乘法器