GAN原理

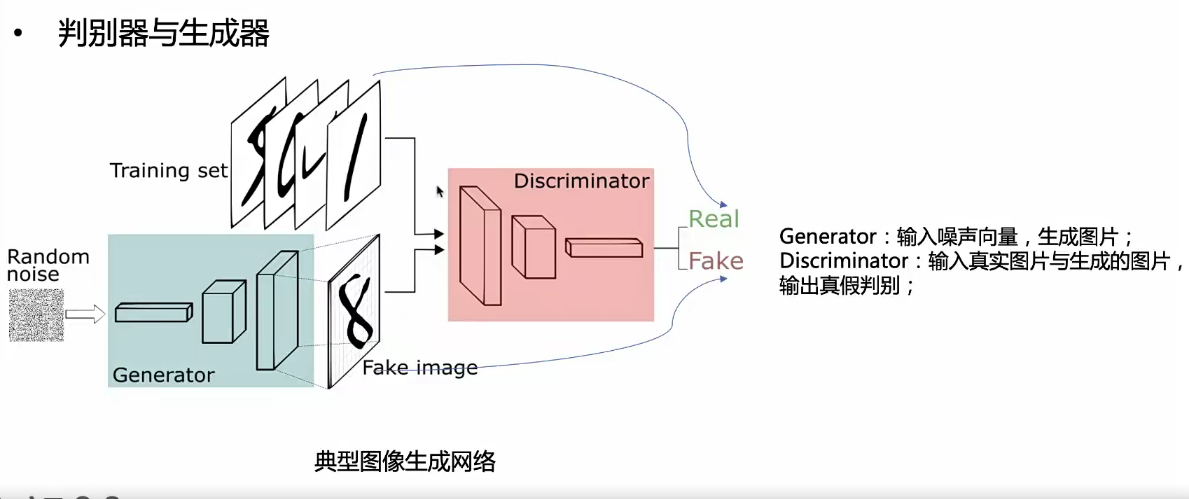
发表于 2023-01-14 更新于 2023-01-17 分类于 AI 阅读次数：本文字数： 652 阅读时长 ≈ 1 分钟

GAN：隐式的生成模型

生成对抗原理

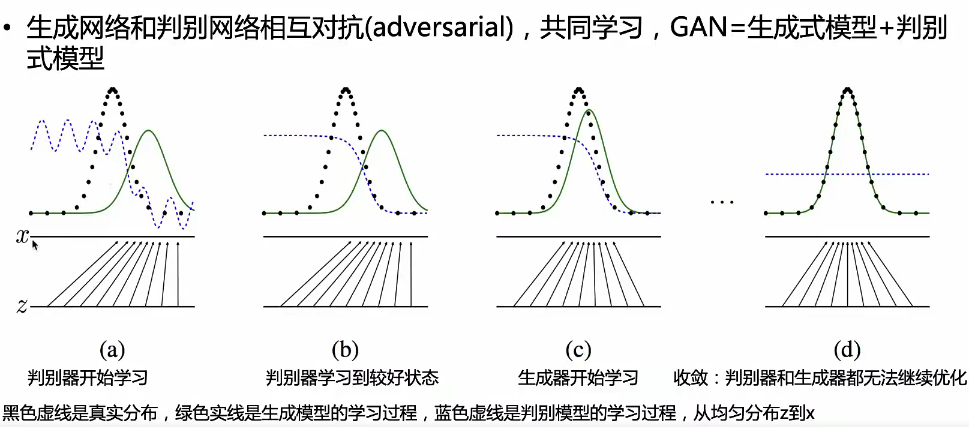
生成器与判别器损失总体优化目标：

\(\min \max V(D, G)=E_{x \sim p_{\text {data }}(x)}[\log \mathrm{D}(\mathrm{x})]+E_{z \sim p_z(z)}[\log (1-\mathrm{D}(\mathrm{G}(\mathrm{z})))]\)

\(E_{x \sim p_{\text {data }}(x)}[\log \mathrm{D}(\mathrm{x})]\) :真实样本输入到判别器的输出 --> 期望这一项越大越好

\(E_{z \sim p_z(z)}[\log (1-\mathrm{D}(\mathrm{G}(\mathrm{z})))]\) :噪声样本输入生成器，再输入判别器以后的样本，应该越小越好，因为用\(1-\mathrm{D}(\mathrm{G}(\mathrm{z}))\) 所以是越大越好。

D的学习目标：D(X)大，D(G(Z))小：

\(\max _\theta \mathbb{E}_{x \sim p_{\text {data }}}[\log D(x)]+\mathbb{E}_{z \sim p_z}[\log (1-D(G(z)))]\)

G的学习目标： D(G(Z))大 \(\min _\theta\mathbb{E}_{z \sim p_z}[\log (1-D(G(z)))]\)

生成器早期的梯度消失问题：

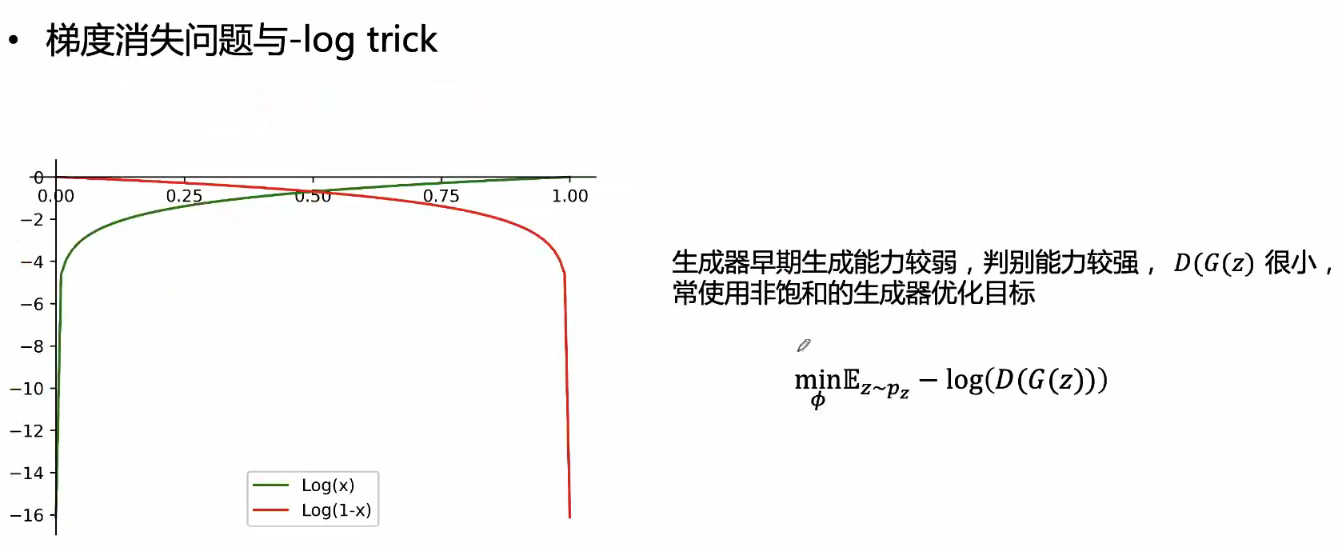
梯度消失问题：

判别器输出是0~1的需要通过sigmoid函数

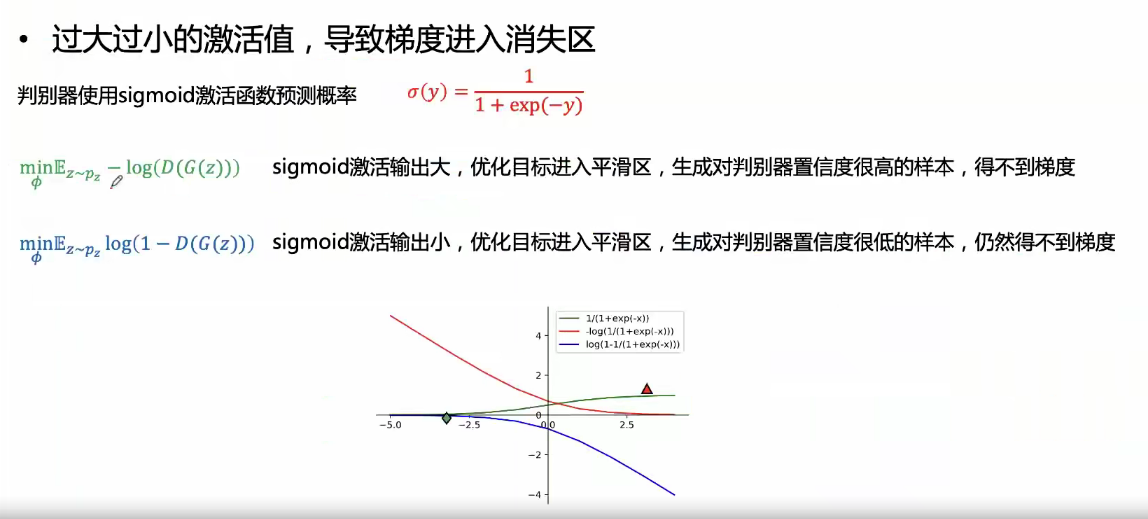
KL散度不对称会造成：